Note 8 B-Trees
Author: Zhen Tong 120090694@link.cuhk.edu.cn Lecturer: Jane YOU
tree structure
Motivation: The deficiency of index order organization is that when the file gets bigger, both the sequential search and index search costs get huge. We can reorganize the file and update indexing for the file, however, it needs extra time to reorganize, and during the reorganization, every operation in the database is pending. We need to find a better way to deal with the file size increasing problem.
Balance Tree Structure (A tree structure is multi-lay indexing)
- The distance from the root to every leaf is the same.
- Every non-leaf node has n/2 to n number of child nodes. (n is the fixed hyperparameter of the tree predefined. Order of the tree)
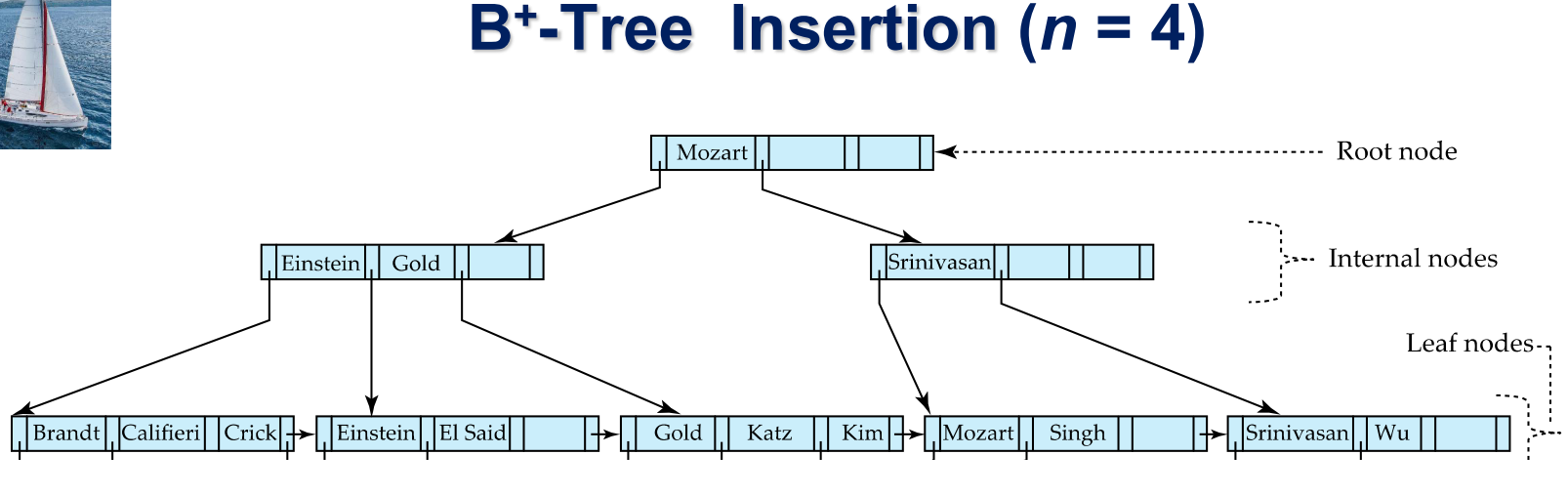
B+Tree structure:
The node structure:
One node has at most n number of pointer, and at most n-1 number of search key . The search key is sequentially sorted, therefore if
一个节点最多有n个pointer最多有n-1个搜索码的值。一个节点的搜索码值是顺序存放的因此,如果.
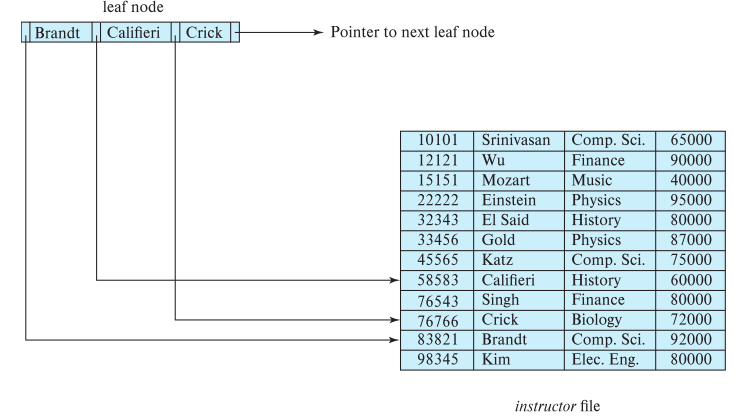
叶节点结构 The leaf node structure:
Each leaf has at most n-1 search key, at least number of search key.
- For example when n = 4, then the leaf node has at most n-1 search key, and at least search key.
The last pointer is linked to the next leaf node.
For every two leaf nodes, if is on the left side of , every search key value in node i is less then all the search key value in node j
If the B+ tree’s index is used for the dense index, then every search key in the B+ tree should appear in somewhere some leaf node
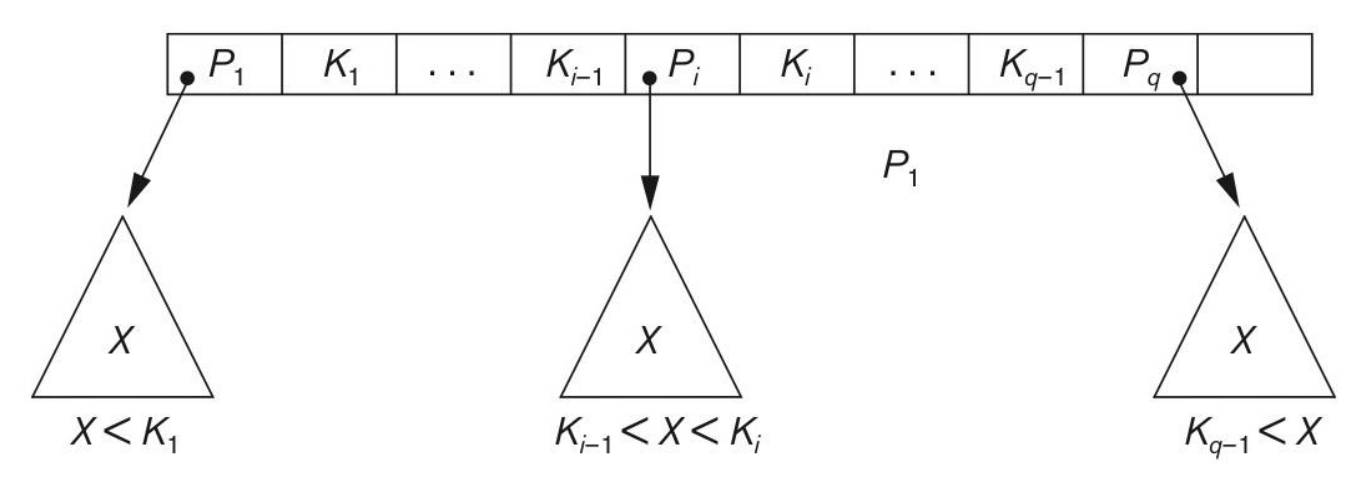
非叶子节点结构 Internal Leaf:
Every node above the leaf node is a multi-layer sparse indexing.
The internal leaf can contain at most n pointers, and at least pointers. All the pointers point to the lower layer node.
Point points to the sub-tree whose search key is all smaller than , and larger or equal to the . You can think as a clapboard.
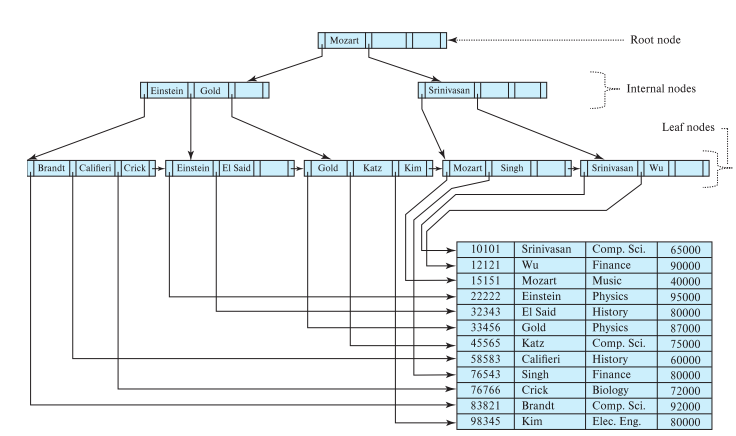
Root node: At least 2 child node, and at most n child node
tree performance
An internal node has numbers of pointers. For a tree with , there are numbers of leaf nodes, which means the search key number is . The maximum depth
- For example, when the B+tree’s node size is designed as the size of a block of disk (4KB), and when n = 100, with numbers of search key. The B+ tree is with depth . Therefore, to search an element you want, you only go through 4 depths.
Average Storage Utilization of B-Tree平均存储利用率
the total number of the search keys of the tree
= the maximum volume of a node, which means a node can contain n/2 to n elements
= the node number in a tree, which changes during your DBMS operation.
is the fullness factor
The volume for any tree is
When f = 1, the tree is full, which means the nodes are fully utilized, and the number of nodes reaches its minimum ,
When f = 1/2, the tree is half-full, every node is taking its most wasteful utilization that half of the space is not used. The number of nodes is maximum,
If we take the number of nodes in a tree as a random variable, and assume the RV
in a continuous uniform distribution, then
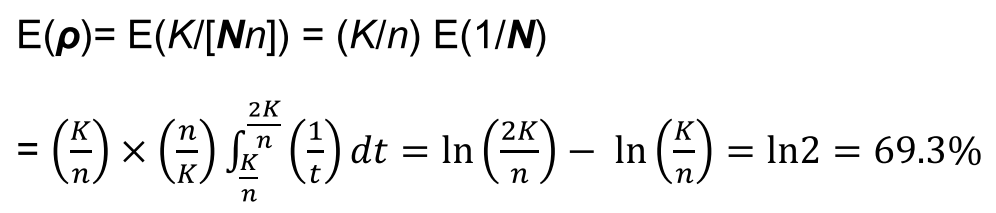
Use fullness factor to generalize the general form:
, (For the B*-Tree, f = ⅔)
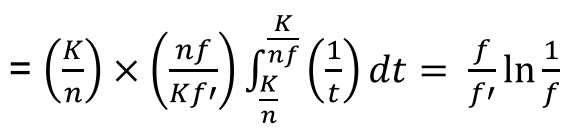
The CDF of is :
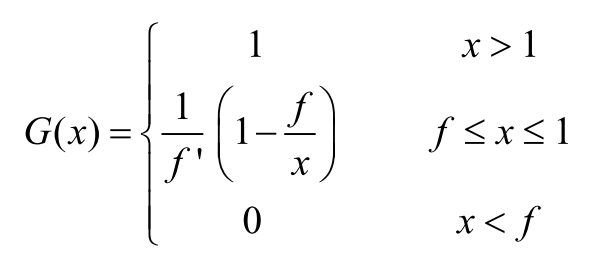
The pdf of is:
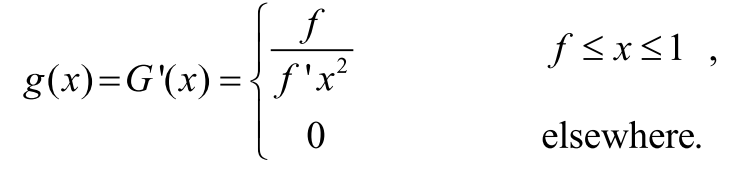
The variance of the Storage Utilization
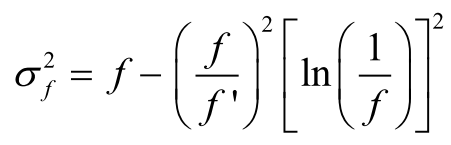
tree update
After we insert or delete some element in the leaf node, the leaf node can be too big, or too small. We need to break up, or merge.
When we need to insert or delete some element, we first need to search where the element is, to ensure the updated tree with a sorted search key, as before.
When we delete some search key, we need to remove all the elements one step to the left, to ensure there is no gap in between.
Insertion
non-leaf node break down
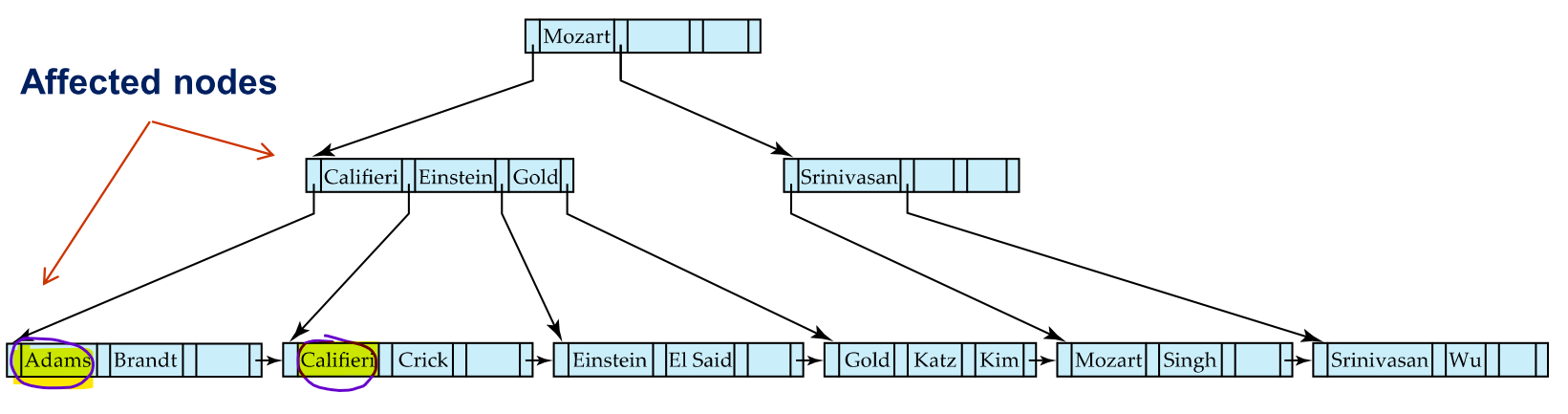
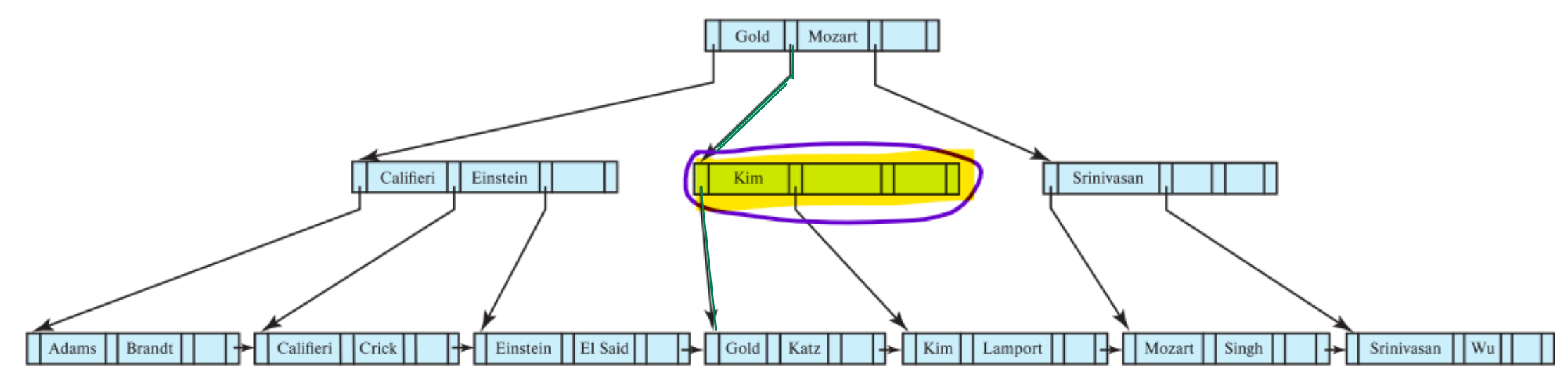
When we insert search K=Lamport
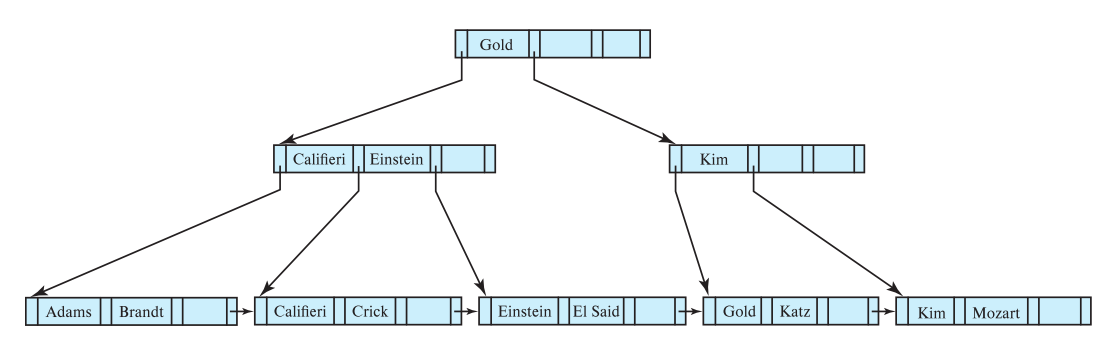
The leaf node of [Gold, Katz , Kim] is the place to insert Lamport. The leaf node meets maximum, and needs to break down

After we break down the leaf node, a new leaf node is created, and we need to add a parent node for Kim. At the same time, Kim’s parent node needs to add a new pointer to Kim’s leaf node.
Delete
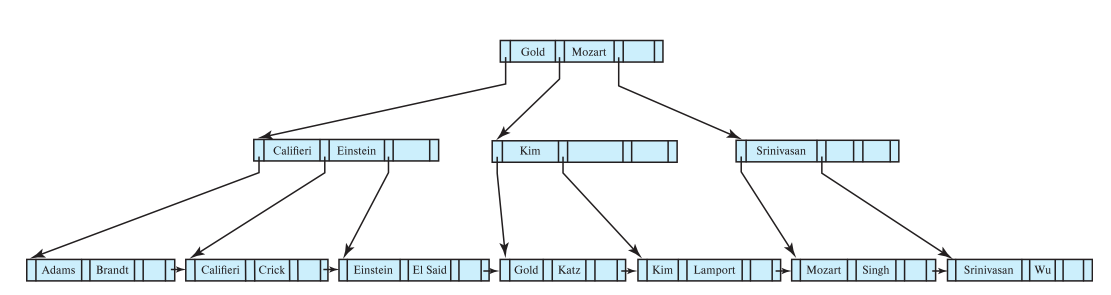
When we want to delete the search key Srinivasan, The parent node of Srinivasan needs to change its search key from Srinivasan to something else. We look up to the grand parent’s node and take Mozart as the new parent. After that, we need to merge the leaf node.
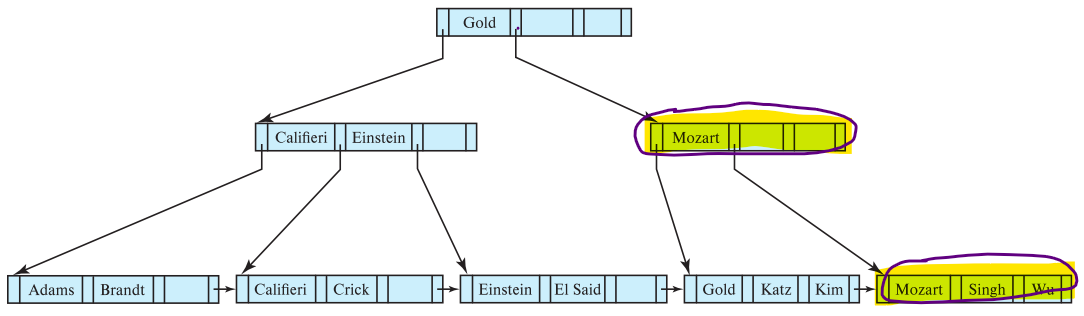
When we want to delete “Singh” and “Wu”
Mozart’s leaf node is less than the minimum(<n/2), and in need of merging other leaves
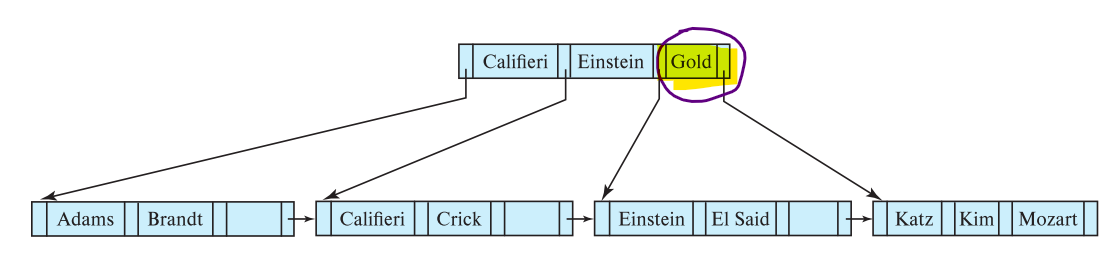
If we delete Gold this time, the depth decreases. The second level node becomes the root node. There is one search Key called Gold in the last, however, it doesn’t point to any available search key. It is still useful because it is a mark for the sorted mark for the following leaf node [Katz, Kim, Mozart]
The cost of inserting and removing a single entry (based on the number of I/O operations) is proportional to the height of the tree
区别
B+Tree File Organization
- The leaf node contains a pointer and search key, and the internal node point to the child node, not to the file record.
B-Tree Index Files
- pointer point to record not only in the leaf node.指向非叶子节点的record
B*-Tree
- A B+ tree with f =⅔,is a B*-Tree
...